En matemáticas, un pseudoprimo de Catalan es un número compuesto n impar que satisface la relación de congruencia:[1]​

( − 1 ) n − 1 2 ⋅ C n − 1 2 ≡ 2 ( mod n ) , {\displaystyle (-1)^{\frac {n-1}{2}}\cdot C_{\frac {n-1}{2}}\equiv 2{\pmod {n}},}

donde Cm denota el m-ésimo número de Catalan. La congruencia también es válida para cada número primo n impar que justifica el nombre de números pseudoprimos para los números compuestos n que lo satisfacen. Su nombre hace referencia al matemático belga Eugène Charles Catalan (1814–1894).

Propiedades

Los únicos pseudoprimos de Catalan conocidos son: 5907, 1194649 y 12327121 (sucesión A163209 en OEIS), siendo los dos últimos cuadrados de primos de Wieferich. En general, si p es un primo de Wieferich, entonces p2 es un pseudoprimo de Catalan.

Referencias

Bibliografía

  • Aebi, Christian; Cairns, Grant (2008). «Catalan numbers, primes and twin primes». Elemente der Mathematik 63 (4): 153-164. doi:10.4171/EM/103. 
  • Catalan pseudoprimes. Investigación en Computación Científica en la Educación de Pregrado.

Numeros de Catalan PDF Conjunto (Matemática) Série de potências

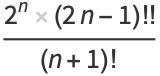
Catalan Number from Wolfram MathWorld

Números en Catalán Como se escriben números en Catalán ⭐2024⭐

‎Numbers in Catalan language on the App Store

Catalan Numbers Naukri Code 360